2D Umbrella Sampling of Alanine-Dipeptide and MBAR¶
Files for this example can be downloaded from here.
This example is located in mdtoolbox_example/umbrella_alad/mbar/.
% this routine calculates free energies of umbrella systems by using MBAR
%% constants
C = getconstants();
KBT = C.KB*300; % KB is the Boltzmann constant in kcal/(mol K)
%% define umbrella window centers
center_phi = -180:15:-15;
center_psi = 0:15:165;
K = numel(center_phi)*numel(center_psi);
umbrella_center = zeros(K, 2);
k = 0;
for i = 1:numel(center_phi)
for j = 1:numel(center_psi)
k = k + 1;
umbrella_center(k, :) = [center_phi(i) center_psi(j)];
end
end
%% read dihedral angle data
for k = 1:K
filename = sprintf('../4_prod/run_%d_%d.dat', umbrella_center(k, 1), umbrella_center(k, 2));
x = load(filename);
data_k{k} = x(:, 2:3);
end
%% evaluate u_kl: reduced bias-factor of umbrella simulation data k evaluated by umbrella l
for k = 1:K
for l = 1:K
spring_constant = 50 * (pi/180)^2; % unit conversion from kcal/mol/rad^2 to kcal/mol/deg^2
u_kl{k, l} = (spring_constant/KBT)*sum(minimum_image(umbrella_center(l, :), data_k{k}).^2, 2);
end
end
%% MBAR: calculate free energies of umbrella systems
f_k = mbar(u_kl);
%% save results
save calc_mbar.mat;
function dx = minimum_image(center, x)
dx = x - center;
dx = dx - round(dx./360)*360;
% this routine calculates 2-D potential of mean force (PMF) from the result of MBAR
%% read MBAR result
load calc_mbar.mat K data_k u_kl f_k KBT;
%% calculate PMF by counting weights of bins under restraint-free condition
% assign 1-dimensional bin index to 2-dimensional data
M_phi = 90;
M_psi = 90;
edge_phi = linspace(-180, 0, M_phi+1);
edge_psi = linspace(0, 180, M_psi+1);
center_phi = 0.5 * (edge_phi(2:end) + edge_phi(1:(end-1)));
center_psi = 0.5 * (edge_psi(2:end) + edge_psi(1:(end-1)));
for k = 1:K
bin_phi = assign1dbin(data_k{k}(:, 1), edge_phi);
bin_psi = assign1dbin(data_k{k}(:, 2), edge_psi);
bin_k{k} = M_psi*(bin_phi-1) + bin_psi;
end
% evaluate PMF of bins
pmf = mbarpmf(u_kl, bin_k, f_k);
% reshape PMF data
pmf2 = zeros(M_phi*M_psi, 1);
pmf2(:) = NaN;
pmf2(1:numel(pmf)) = pmf;
pmf2 = KBT*pmf2; % convert unit from KBT to kcal/mol
pmf2 = pmf2 - min(pmf2(:));
pmf = reshape(pmf2, M_psi, M_phi);
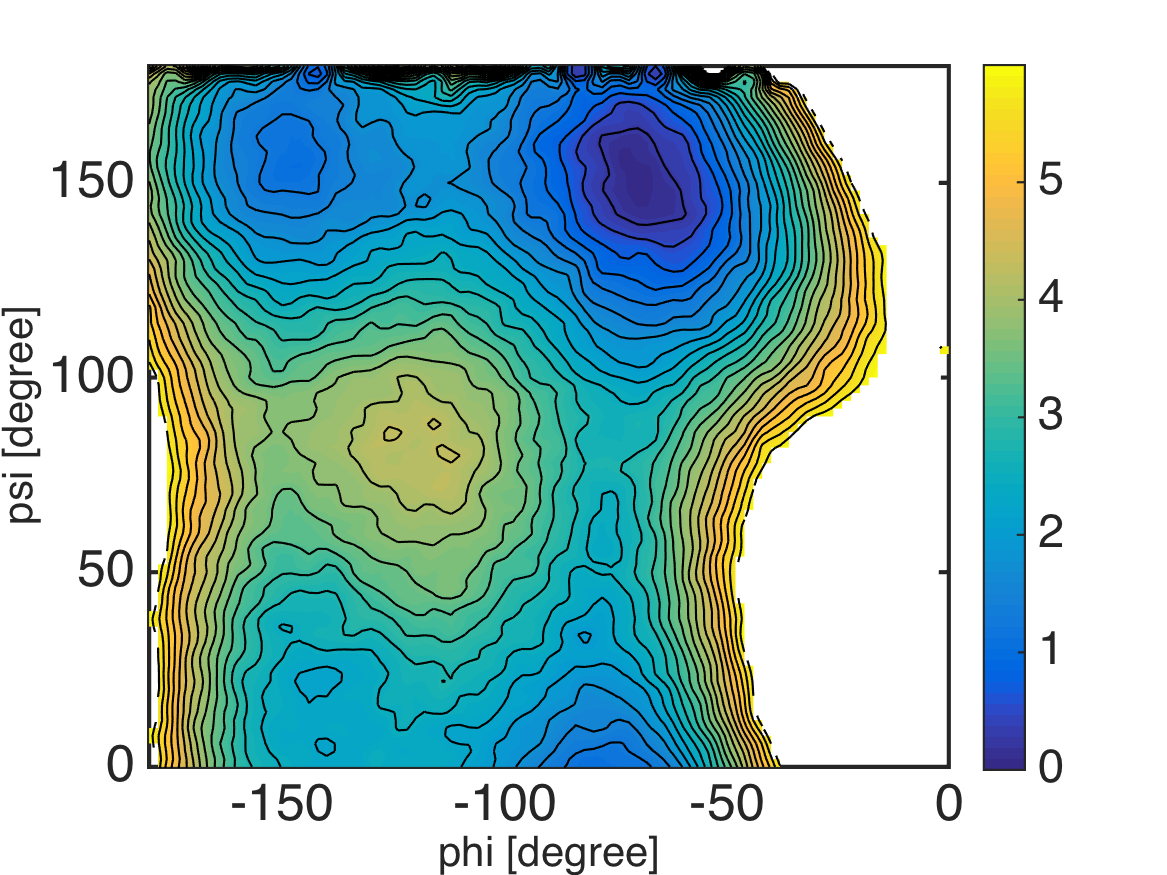
%% visualization
landscape(center_phi, center_psi, pmf, 0:0.25:6); colorbar;
xlabel('phi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
ylabel('psi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
exportas('pmf_histogram');
% this routine calculates 2-D potential of mean force (PMF) from the result of MBAR
%% read MBAR result
load calc_mbar.mat K data_k u_kl f_k KBT;
%% evaluate weights of data under restraint-free condition
[~, w_k] = mbarpmf(u_kl, [], f_k);
%% calculate PMF by using kernel density estimation
% collect scattered data with weights
data = [];
for k = 1:K
data = [data; data_k{k}];
end
weight = [];
for k = 1:K
weight = [weight; w_k{k}];
end
% evaluate PMF by using a kernel density estimator
center_phi = -180:2.0:0;
center_psi = 0:2.0:180;
pmf = calcpmf2d(data, center_phi, center_psi, [2.0 2.0], [360 360], weight);
pmf = pmf*KBT; % convert unit from KBT to kcal/mol
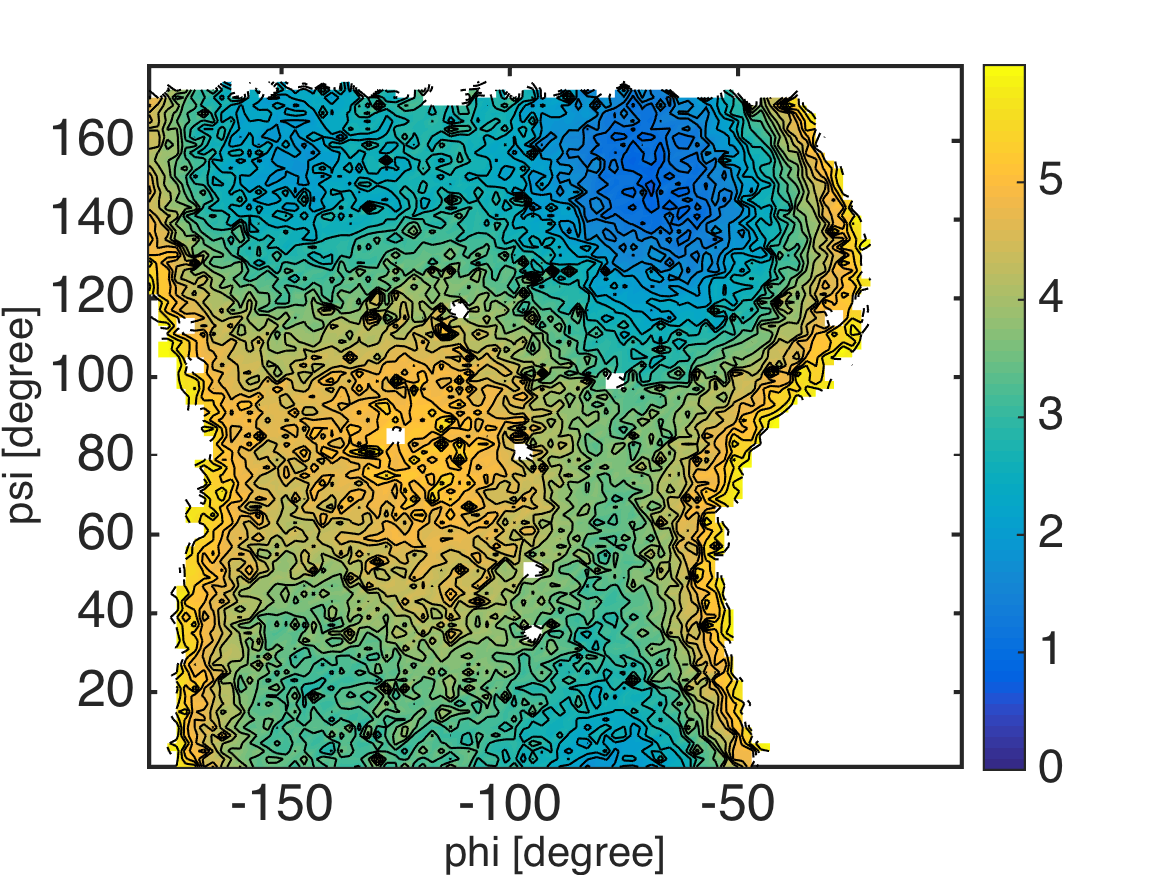
%% visualization
landscape(center_phi, center_psi, pmf, 0:0.25:6); colorbar;
xlabel('phi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
ylabel('psi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
exportas('pmf_ksdensity');