1D Umbrella Sampling of Tri-Alanine and dTRAM¶
Files for this example can be downloaded from here.
This example is located in mdtoolbox_example/umbrella_alat/dtram/.
% this routine calculates the Potential of Mean Force (PMF) from umbrella sampling data by using dTRAM
%% setup constants
C = getconstants();
KBT = C.KB*300; % KB is the Boltzmann constant in kcal/(mol K)
%% umbrella window centers
umbrella_center = 0:3:180;
K = numel(umbrella_center); % number of umbrella window
%% define edge for bin
M = 80; % number of Markov sates
edge = linspace(-1, 181, M+1);
bin_center = 0.5 * (edge(2:end) + edge(1:(end-1)));
%% bias-factor
% bias_km: bias-factor for k-th umbrella-window evaluated at m-th bin-center
bias_km = zeros(K, M);
for k = 1:K
for m = 1:M
spring_constant = 200 * (pi/180)^2; % conversion of the unit from kcal/mol/rad^2 to kcal/mol/deg^2
bias_km(k, m) = (spring_constant./KBT)*(minimum_image(umbrella_center(k), bin_center(m))).^2;
end
end
%% read dihedral angle data
data_k = {};
for k = 1:K
filename = sprintf('../3_prod/run_%d.dat', umbrella_center(k));
x = load(filename);
data_k{k} = x(:, 2);
end
%% calculate count matrix for transition between bins
index_k = {};
for k = 1:K
index_k{k} = assign1dbin(data_k{k}, edge);
end
c_k = {};
for k = 1:K
c_k{k} = msmcountmatrix(index_k{k}, 1, M);
end
%% dTRAM
pmf = dtram(c_k, bias_km);
pmf = KBT*pmf;
pmf = pmf - pmf(1);
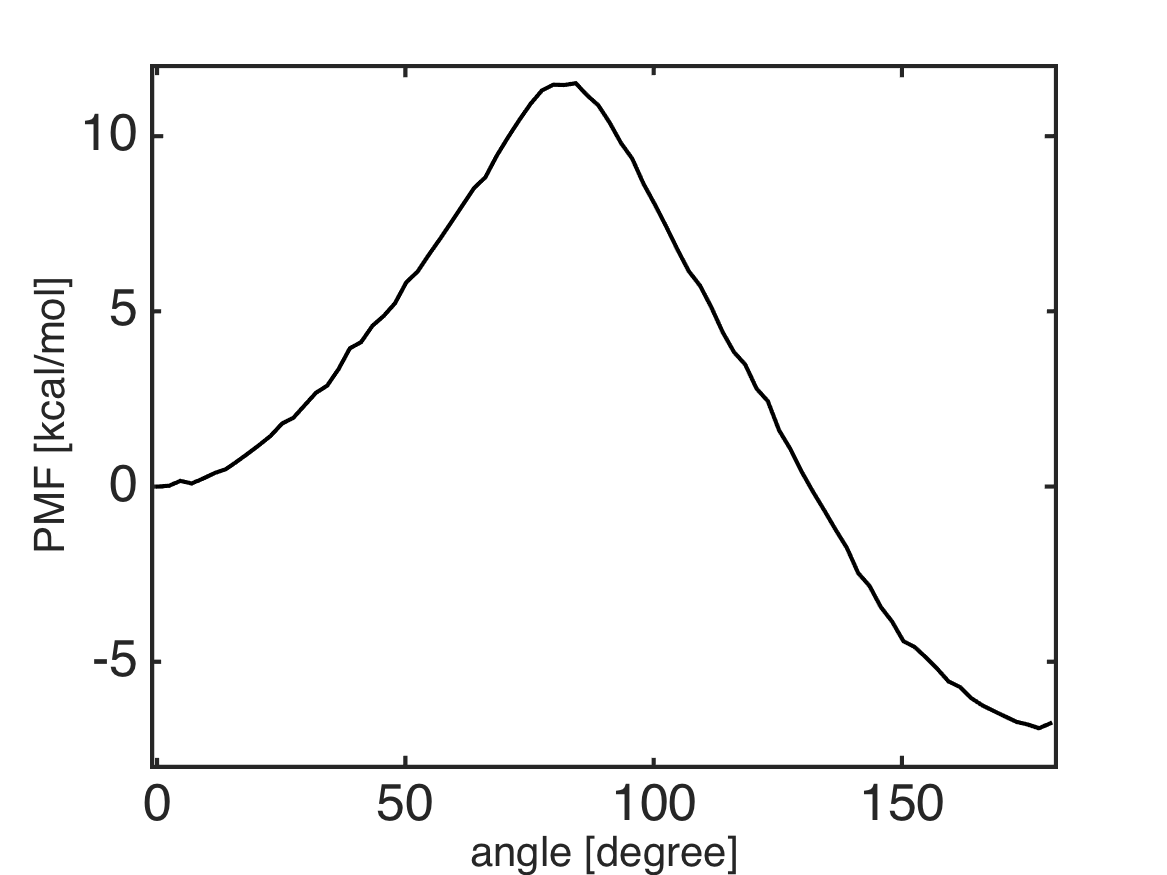
%% plot the PMF
hold off
plot(bin_center, pmf, 'k-');
formatplot
xlabel('angle [degree]', 'fontsize', 20);
ylabel('PMF [kcal/mol]', 'fontsize', 20);
axis([-1 181 -8 12]);
exportas('analyze')
hold off
%% save results
save analyze.mat;
function dx = minimum_image(center, x)
dx = x - center;
dx = dx - round(dx./360)*360;