Conventional MD of Alanine-Dipeptide and 2D PMF surface¶
Files for this example can be downloaded from here.
This example is located in mdtoolbox_example/md_alad/pmf/.
We calculate the surface of potential of mean force (PMF) in a 2-dimensional dihedral angle space. Molecular dynamics trajectory of alanine-dipeptide solvated in explicit water models is used for the demonstration.
First, we extract dihedral angles from the trajectory:
%% read data
trj = readnetcdf('../3_prod/run.nc');
%% define atom indices for dihedral angles
index_phi = [5 7 9 15];
index_psi = [7 9 15 17];
%% calculate dihedral angles
phi = calcdihedral(trj, index_phi);
psi = calcdihedral(trj, index_psi);
%% convert the unit from radian to degree
phi = phi.*180./pi;
psi = psi.*180./pi;
Next, the probability density function (PDF) in the
2-dimentional dihedral space is estimated from the scattered data
(phi and psi). This can be done by using the bivariate kernel
density estimation (ksdensity2d.m) which is called in
calcpmf2d.m routine.
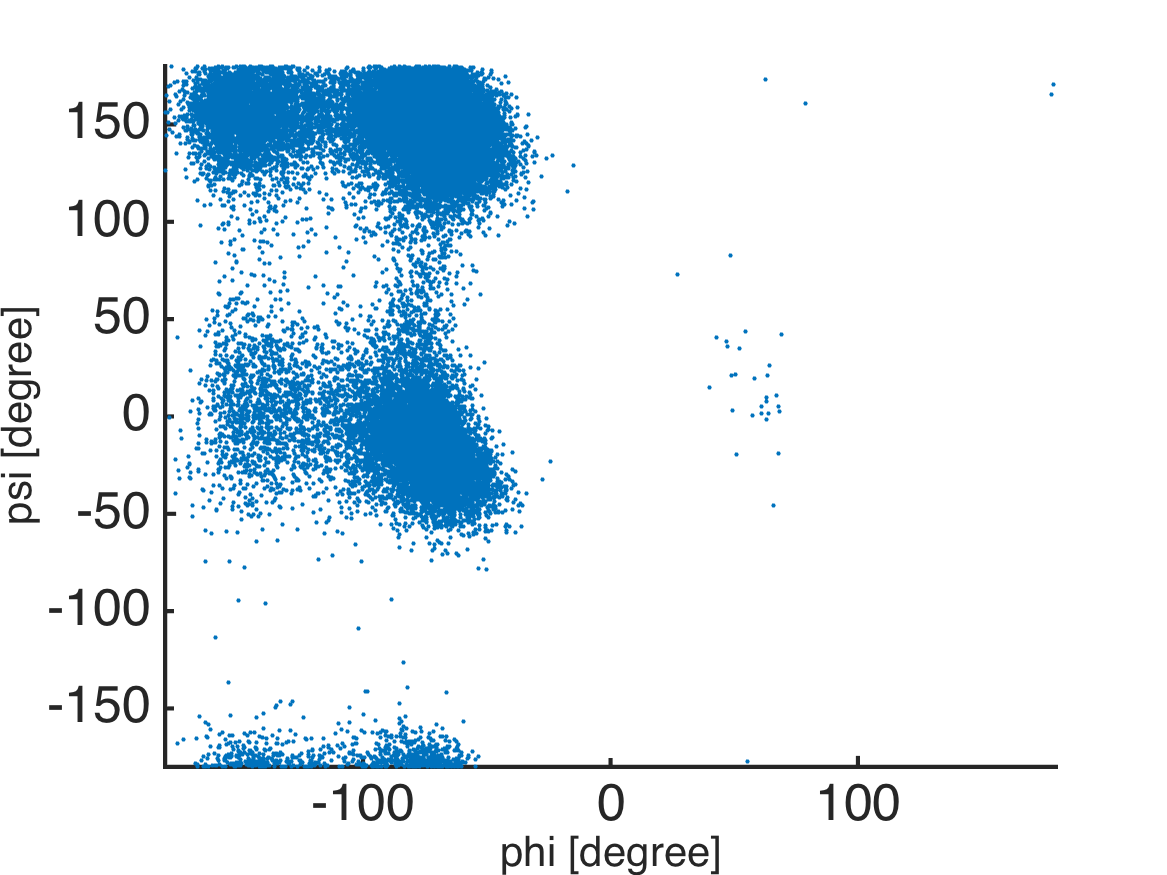
%% scattered plot of the dihedral angles
scatter(phi, psi, 5, 'filled');
axis([-180 180 -180 180]); axis xy;
formatplot2
xlabel('phi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
ylabel('psi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
exportas('scatter');
%% calculate PMF and visualize the surface
xi = -180:2:180; % grids in x-axis
yi = -180:2:180; % grids in y-axis
pmf = calcpmf2d([phi psi], xi, yi, [3.0 3.0], [360 360]);
s = getconstants(); % get Boltzmann constant in kcal/mol/K
T = 300.0; % set temperature
pmf = s.KB*T*pmf; % convert unit from KBT to kcal/mol
%% visualization
landscape(xi, yi, pmf, 0:0.25:6); colorbar;
axis([-180 180 -180 180]);
xlabel('phi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
ylabel('psi [degree]', 'FontSize', 20, 'FontName', 'Helvetica');
exportas('pmf');
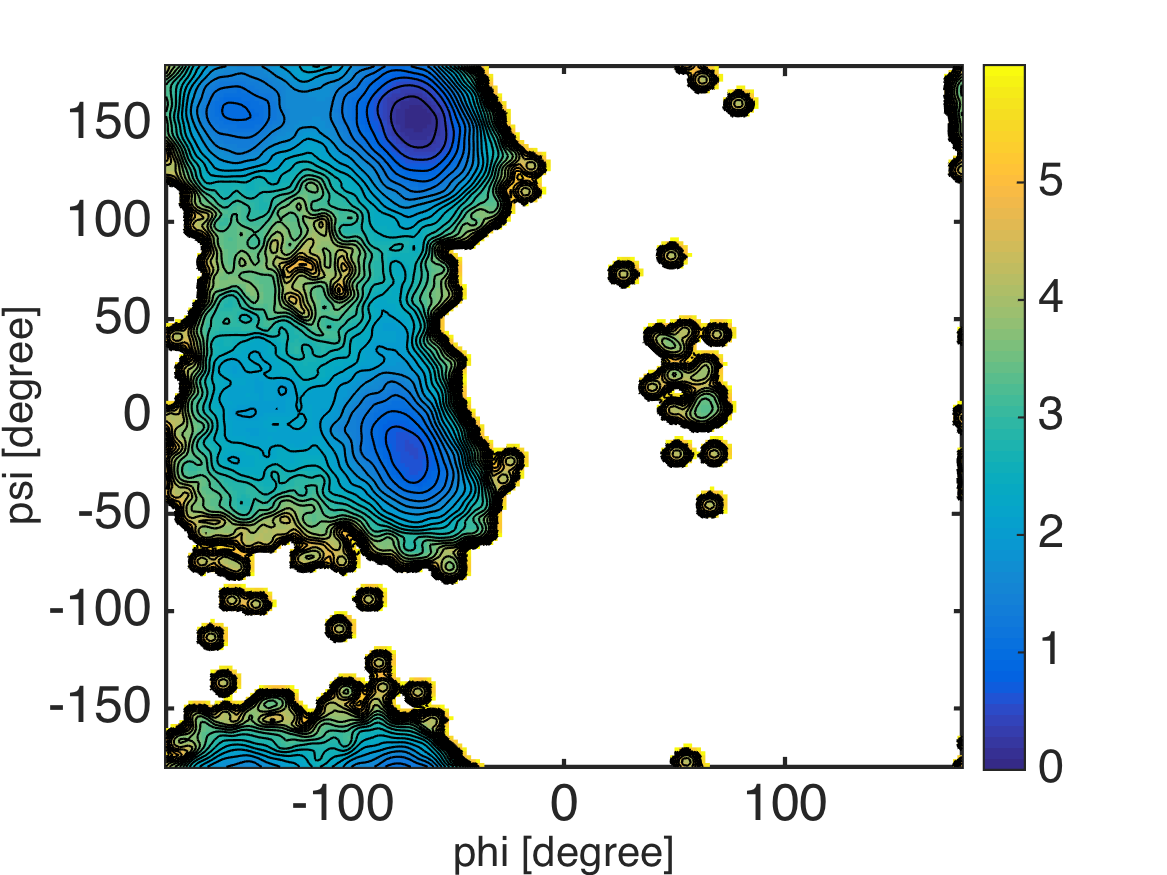
Note that the kernel density estimator tends to broaden the “true” PDF surface by a convolution with a Gaussian kernel. So, we should be careful especially when interested in small dips or barrier heights on the surface.